Conceptos y aplicaciones
El concepto de derivada es uno de los dos conceptos centrales del cálculo infinitesimal. El otro concepto es la "antiderivada" o integral; ambos están relacionados por el teorema fundamental del cálculo. A su vez, los dos conceptos centrales del cálculo están basados en el concepto de límite, el cual separa las matemáticas previas, como el Álgebra, la Trigonometría o la Geometría Analítica, del Cálculo. Quizá la derivada es el concepto más importante del Cálculo Infinitesimal.
La derivada es un concepto que tiene variadas aplicaciones. Se aplica en aquellos casos donde es necesario medir la rapidez con que se produce el cambio de una magnitud o situación. Es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología, o en ciencias sociales como la Economía y la Sociología. Por ejemplo, cuando se refiere a la gráfica de dos dimensiones de f, se considera la derivada como la pendiente de la recta tangente del gráfico en el punto x. Se puede aproximar la pendiente de esta tangente como el límite cuando la distancia entre los dos puntos que determinan una recta secante tiende a cero, es decir, se transforma la recta secante en una recta tangente. Con esta interpretación, pueden determinarse muchas propiedades geométricas de los gráficos de funciones, tales como concavidad o convexidad.
Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Por ejemplo, una función no tiene derivada en los puntos en que se tiene una tangente vertical, una discontinuidad o unpunto anguloso. Afortunadamente, gran cantidad de las funciones que se consideran en las aplicaciones son continuas y su gráfica es una curva suave, por lo que es susceptible de derivación.
Las funciones que son diferenciables (derivables si se habla en una sola variable), son aproximables linealmente.
[editar]Introducción geométrica a las derivadas
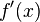 representa la pendiente de la recta tangente a la gráfica de
representa la pendiente de la recta tangente a la gráfica de  en el punto
en el punto  .
.En términos geométricos, esta pendiente 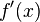 es "la inclinación" de la línea recta que pasa justo por encima del punto
es "la inclinación" de la línea recta que pasa justo por encima del punto 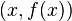 y que es tangente a la gráfica de
y que es tangente a la gráfica de  .
.
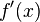 es "la inclinación" de la línea recta que pasa justo por encima del punto
es "la inclinación" de la línea recta que pasa justo por encima del punto 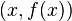 y que es tangente a la gráfica de
y que es tangente a la gráfica de  .
.Al identificar dos puntos muy cercanos en la gráfica y al unirlos mediante una línea recta, una pendiente queda visualizada. Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, la recta se parece más a una recta tangente a la gráfica y su pendiente se parece más a la pendiente de una recta tangente.
Notamos que esta pendiente coincide con la rapidez con que aumenta el valor de la función en cada punto. Dicho de otra manera, si la pendiente en un punto es muy grande, entonces el valor de la función en ese punto crece muy deprisa; si la pendiente es muy pequeña, entonces el valor de la función crece muy despacio en ese punto.
Es decir, tanto la pendiente de la recta tangente como la rapidez de crecimiento en un punto  de una función
de una función  está dado por
está dado por 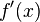 .
.
 de una función
de una función  está dado por
está dado por 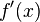 .
.No todas las funciones poseen derivada. Desde el punto de vista geométrico esto se puede deber a varios motivos. Por ejemplo hay funciones donde se da el caso de que por un mismo punto pasan muchas rectas tangentes(por ejemplo la función valor absoluto en el punto 0) y no es posible definir de manera única la pendiente a la recta tangente. También se da el caso de que no se puede definir la pendiente a una recta tangente en una función que no es continua. Incluso hay funciones donde cualquier recta que pase por uno de sus puntos intersecta en una infinidad de puntos muy cercanos y por tanto no hay recta tangente.
Las funciones que poseen derivada se llaman diferenciables.
Conocer la derivada de una función diferenciable por lo general resulta una tarea sencilla utilizando las técnicas de derivación desarrolladas por Gottfried Leibniz e Isaac Newton, las cuales permiten conocer las derivadas de muchas de las funciones de interés frecuente o bien, simplificar el trabajo para encontrar derivadas menos comunes.
Condiciones de continuidad de una función
Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir,  , y usando la expresión Δy + y = f(Δx + x), queda
, y usando la expresión Δy + y = f(Δx + x), queda  donde en este caso, f(x) = y. Ello quiere decir que
donde en este caso, f(x) = y. Ello quiere decir que 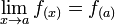 , y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
, y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
 , y usando la expresión Δy + y = f(Δx + x), queda
, y usando la expresión Δy + y = f(Δx + x), queda  donde en este caso, f(x) = y. Ello quiere decir que
donde en este caso, f(x) = y. Ello quiere decir que 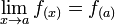 , y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
, y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con es continua en el punto a.
es continua en el punto a.
Condición no recíproca
La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean equivalentes pero las derivadas laterales no; en este caso la función presenta un punto anguloso en dicho punto.
Un ejemplo puede ser la función valor absoluto (también llamada módulo) en el punto 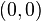 . Dicha función es equivalente a la función partida
. Dicha función es equivalente a la función partida 
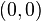 . Dicha función es equivalente a la función partida
. Dicha función es equivalente a la función partida 
Para valores infinitamente cercanos a 0, por ambas ramas, el resultado tiende a 0. Y el resultado en el punto 0 es también 0, por lo tanto es continua. Sin embargo, las derivadas resultan 

Cuando  vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.
vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.
 vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.
vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.De manera informal, si el gráfico de la función tiene puntas agudas, se interrumpe o tiene saltos, no es derivable.
 .
.
No hay comentarios:
Publicar un comentario